Department Research Topics

Object oriented data analysis is the statistical analysis of populations of complex objects. In the special case of functional data analysis, these data objects are curves, where a variety of Euclidean approaches, such as principal components analysis, have been very successful. Challenges in modern medical image analysis motivate the statistical analysis of populations of more complex data objects that are elements of mildly non‐Euclidean spaces, such as lie groups and symmetric spaces, or of strongly non‐Euclidean spaces, such as spaces of tree‐structured data objects. These new contexts for object oriented data analysis create several potentially large new interfaces between mathematics and statistics. The notion of object oriented data analysis also impacts data analysis, through providing a framework for discussion of the many choices needed in many modern complex data analyses, especially in interdisciplinary contexts.

The main idea of Generalized Fiducial Inference is to carefully transfer randomness from the data to the parameter space using an inverse of a data-generating equation without the use of Bayes’ theorem. The resulting generalized fiducial distribution (GFD) can then be used for inference. Research focuses on

1) Definition and theoretical properties of generalized fiducial inference

2) Application of generalized fiducial inference to statistical problems of practical interest

3) Model selection and non-parametric models using the generalized fiducial distribution

4)  Practical computation of fiducial distribution

Networks describe pairwise relationships (or interactions) between a set of objects.  Mathematically, a network is a graph where the objects are treated as vertices (nodes)  and an edge (link) is placed between two vertices if they are related to each other. Networks and network data are ubiquitous: examples include brain networks from neuroscience, Facebook and Twitter networks, the internet, social networks, protein- and gene-interaction networks, and ecological networks of interacting species.

The probabilistic and statistical analysis of networks has been motivated by, and made contributions to, modeling and understanding complex systems in a variety of fields. Topics directly related to the research of the department include:

1. Community detection: In community detection, the goal is to identify in a given network a group of vertices, called a community,  with the property that the vertices in the community are highly interconnected, but have relatively few connections with vertices outside the community. Community detection, which is related to the problem clustering, is an important exploratory tool for identifying structure in large networks, and is a common first step in network analysis.
2. Diffusion of information through networks: Many networks (especially information networks such as the Internet at the router level) deal with the transmission of flow between different parts of the network. The department has expertise in understanding models of diffusion of information through networks including probabilistic models for such diffusion (e.g. epidemic models) structural properties of optimal paths etc.
3. Change point detection for networks: In applications, one of the most fascinating directions for research is dynamic networks i.e. networks evolving in time. The department has expertise in developing models for such data, including the detection of change points where some intrinsic characteristic determining the evolution rules of the network changes.

In many applications, one is often interested in asking how long it takes for a Markov process to converge to its stationary distribution (if it exists). One could think of this problem as follows: run two copies of the process on the same space, one starting from a point and the other from the stationary distribution,  and see how long it takes for the processes to meet. This method of constructing two processes with prescribed marginal distributions jointly on the same space is referred to as `coupling Markov processes.’ For studying convergence rates to
stationarity, the idea is to incorporate useful dependencies between the two processes (while preserving their marginals) and make them meet as quickly as possible. This meeting time, known as the coupling time, can be used to quantify the convergence rates. Note that this method can be thought of as an optimization problem (minimize coupling time) with constraints (the marginal distributions) and thus lies at the fertile intersection of probability and optimization (two strong communities housed by our department). In addition, couplings can also be used to explore the geometry of the underlying space in which the Markov process lives. We are exploiting couplings to understand exotic geometries (like sub-Riemannian geometries) using purely probabilistic tools. Another new area we are currently exploring using couplings is to study local convergence to equilibrium for high-dimensional Markov processes. As an example, consider a queueing network with many servers. Although the whole network can take really long to stabilize, in many situations, simulations suggest that the queue lengths of a smaller subset of servers stabilize much faster. Although this local dynamic is possibly non-Markovian, couplings provide a tractable way to study this question.

Theory of large deviations is a well-established field whose basic mathematical foundations were laid in the classical works of Donsker and Varadhan. The topic has been extensively studied and now there are several excellent books and monographs on the topic. The central goal in this theory is the study of precise decay rates of probabilities of rare events associated with a given stochastic system as a certain scaling parameter approaches its limit. This basic problem of characterization of decay rates of probabilities arises in a large number of problems and is a central theme in probability theory. Such problems go beyond the core area of probability theory and applications of the theory abound in all the physical and biological sciences and also in engineering, computer science, economics, finance, and social sciences. Large deviations theory not only gives asymptotic bounds for probabilities but also techniques for constructing efficient accelerated Monte-Carlo methods for estimating probabilities of rare events.  Our research focuses on a broad range of problems in the theory and applications of large deviations, including problems in infinite dimensional stochastic dynamical systems, interacting particle systems, systems with multiple temporal and spatial scales etc.

Extreme value theory refers to a class of probabilistic and statistical methods aimed at understanding the distributions of extremes in random sequences and stochastic processes. In its simplest form, extreme value theory for univariate data leads to a class of “extreme value distributions” that were originally developed for IID data but also shown to be applicable for many cases where the data are dependent or do not all have the same distribution. This theory has been applied in many fields including reliability and strength of materials, finance, and environmental extremes. A particularly popular current application is to climate extremes, in particular, understanding to what extent climate extremes are becoming more frequent and can be attributed to the human influence on climate.

In recent years there have been many extensions to multivariate and spatial problems of extremes. Max-stable processes are a class of stochastic processes particularly well suited to studying extremes in time series and spatial data, but there are challenging problems of characterizing max-stable processes and performing statistical inference. Modern extreme value theory fits well within the paradigm of statistical methods for large high-dimensional datasets but it still poses many very distinctive problems.

Nonparametric methods do not require the user to know what particular distribution or model produced the data at hand. Such methods are needed when the statistician lacks prior knowledge of the underlying data-generating process, or when the statistician wants a robust corroborator for results from a parametric analysis of the data.

One use case of nonparametrics is resampling. In order to make statistical inferences, one needs information about the sampling distribution of the statistic at hand. Although in many situations the sampling distribution is known to be approximately normal, there are many other cases where the sampling distribution cannot be derived theoretically, and may be quite non-normal, for example if the statistic is extremely complicated or if the observations are not independent. Resampling methods, such as the jackknife and the bootstrap, allow the statistician to nonparametrically estimate sampling distributions in these difficult situations, essentially by re-using the observed data.

Queueing systems are a big part of modern life. They are everywhere we go — physically (supermarkets, hospitals, banks, airports, etc.) or virtually (call centers, communication or computer networks, etc.). Mathematical modeling and analysis of queueing systems have been the focus of operations researchers for more than half a century. Nevertheless, advances in computing technology, manufacturing and service processes continue to bring about new challenges to efficient management of queueing systems.

Healthcare delivery, even for outpatients, requires the use of expensive and many times scarce resources, which can range from physicians and nurses to MRI and dialysis machines. Therefore, it is essential that these resources are used efficiently, in a way they are highly utilized but are not overworked to the point of negatively impacting the quality of service or adding significant financial costs. At its core, this is a problem of matching patient demand with service supply. Just to illustrate the main idea, consider an outpatient clinic with a single physician. Patient demand is typically random and non-stationary and although service capacity is more or less fixed, there is some control over how many patients can be seen every day. For example, a clinic can work overtime with some additional cost or overbook patients and see more patients during regular working hours possibly in the expense of service quality. The clinic would also typically try to regulate the fluctuations in day-to-day patient demand by offering appointments in the future. However, while appointments help smooth out the demand, a very common problem is no-shows and no-shows, while depending on many factors, are typically more likely the longer the patients have to wait for their appointments to arrive. The question then is how the clinic should simultaneously decide what capacity to offer, how to schedule patients within a day, and how to schedule appointments into the future. Further complexities arise if one were to consider multiple providers working at the same clinic, patient preferences for appointment dates and times as well as providers and continuity of care, patients requiring multiple appointments (as in the case of physical therapy or dialysis) etc.

Hospitals are highly complex systems and as a result they provide researchers an endless stream of important, interesting, and challenging research problems. In many cases, a patient’s visit to a hospital typically starts in the emergency department (ED) or in the surgery unit as an elective patient. The patient goes through different stages of “service” during her stay in the hospital. Viewed from a distance, the ED-Hospital system can be seen as a complex network of queues and it is tempting to draw an analogy with a production system, which also can be seen as a network of queues. Nevertheless, while the analogy works up to a certain point and both types of systems are difficult to analyze, healthcare operations pose significant additional challenges. At the top of these challenges is the fact that a hospital typically has multiple objectives some of which might in fact be conflicting with each other. A hospital aims to give the best possible care to its patients – which is a vague goal by itself as it has to entail giving priority to patients with life threatening injuries along with delivering an overall short waiting times to the rest of the patients – but also reduce costs, make profits, and better compete with the other hospitals. There are complex interactions among the “servers.” A server might correspond to different entities (a bed, a diagnostic equipment, a nurse, a physician etc.) depending on the service stage and more than one type of server might be needed at the same time for the execution of any given part of service.

Mass-casualty events such as natural disasters and terrorist attacks are not common occurrences but when they happen they can easily overwhelm emergency response systems in the affected area. Below are two examples of resource allocation problems:

1. Mass-casualty triage: Following a mass-casualty event, one of the most challenging decisions faced by emergency responders is to prioritize patients competing for scarce resources such as ambulances and operating rooms. In medical terminology, the practice of categorizing and prioritizing patients according to their health conditions is called triage. The most commonly used triage policy in the U.S. classifies patients into four criticality groups and largely ignores the level of resource limitations with respect to the size of the event. With the objective of developing effective resource-based triage rules, our research group formulated multiple mathematical models that capture the main tradeoff between prioritizing patients who are in more critical conditions and those who are either faster to save or more likely to survive.
2. Patient distribution to hospitals: In the aftermath of a mass-casualty event, another major decision that heavily affects the outcome of the response effort is the distribution of casualties among multiple hospitals in the area. The most common practice is to transfer all patients to the nearest hospital, which is easy-to-implement and intuitive. However, such a simplistic approach to patient distribution proved to result in poor outcomes in past disasters. For a more effective policy, one needs to incorporate several factors into the decision such as travel times to hospitals, number of ambulances, hospital service capabilities, and hospital census levels.

Large-scale nonconvex optimization is a core step in many machine learning and statistical learning applications, including deep learning, reinforcement learning, and Bayesian optimization. Due to its high-dimensionality and expensive oracle evaluations, e.g. in the big data regime, stochastic gradient descent (SGD) algorithms are often employed for these applications. Recently, there are at least two leading research trends in developing SGD algorithms. The first one essentially relies on the classical SGD scheme but applies it to a specific class of problems by further exploiting problem structures to obtain better performance. The second trend is based on variance reduction techniques. While variance reduction methods often have better oracle complexity bounds than SGD-based methods, their performance, e.g. on neural network training models, is not satisfactory. This observation leads to a belief that there is a gap between theoretical guarantees and practical performance in SGDs. In practice, many algorithms implemented for deep learning come from the first trend, but intensively exploit adaptive strategies and momentum techniques to improve and stabilize performance.

This research topic aims to study both the theoretical and practical aspects of stochastic gradient methods, with both standard and variance reduction methods relying on some recent universal concepts such as relative smoothness and strong convexity. It also concentrates on developing a new approach called hybrid stochastic optimization methods to deal with large-scale nonconvex optimization problems. In addition to theoretical and algorithmic development, implementation and applications in machine learning will also be considered.

Self-concordance is a powerful mathematical concept introduced by Y. Nesterov and A. Nemirovskii in 1990s and widely used in Interior-Point methods. Recently, it has been recognized that the class of self-concordant functions also covers many important problems in statistics and machine learning such as graphical learning, Poisson image processing, regularized logistic regression, and distance weighted discrimination. This research topic focuses on studying the self-concordant concept and its generalizations to broader classes of functions. It also investigates theoretical foundations beyond self-concordance and develops novel solution methods to solve both convex and nonconvex optimization problems involving generalized self-concordant structures where existing methods may not have theoretical guarantees or become inefficient. It also seeks new applications in different domains where such generalized self-concordance theory applies.

Convex optimization with complex structures such as linear and nonlinear constraints and max structures remains challenging to solve in large-scale settings. These problems have various applications in almost every domain. Representative examples include network optimization, distributed optimization, transportation, basis pursuit, and portfolio optimization. State-of-the-art first-order methods for solving these problems consist of [accelerated] gradient descent-based, primal-dual, augmented Lagrangian (e.g. alternative direction method of multipliers (ADMM)), coordinate descent, and stochastic gradient descent-based methods. While these methods have been widely used in practice and have shown great performance, their theoretical aspects on constrained and min-max settings are not really well-understood, especially in adaptive algorithmic variants. The objective of this topic is to develop a class of nonstationary first-order methods where the algorithmic parameters are updated adaptively under the guidance of theoretical analysis. Such new algorithms are expected to have better theoretical guarantees than existing methods. It also focuses on understanding the gap between practice and theoretical guarantees in existing methods such as primal-dual schemes, ADMM, and their variants. In addition, it also aims at customizing the proposed methods to concrete applications and their practical implementations.

Semidefinite programs (SDPs) are some of the most useful, versatile, and exciting optimization problems to emerge in the last few decades. SDPs consist of a semidefinite matrix variable, a linear objective function, and linear constraints.

For example, the set of correlation matrices – n by n matrices with all ones on the diagonal – is the feasible set of a particular SDP.

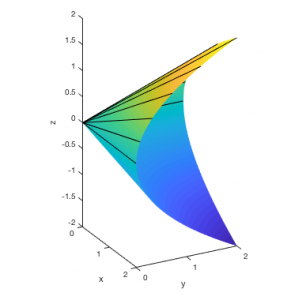
Why are SDPs exciting? Firstly, they have beautiful geometry, as seen in the pictures shown here.

Second, as said before, they are very useful. Third, they exhibit interesting odd behaviors that are not present in linear programs. For example, they may not attain their optimal values.

Recent research in the department has focused on trying to understand these odd behaviors. Interestingly, it turned out that we can use mostly elementary row operations (coming from Gaussian elimination) to bring SDPs into a form, so the odd behaviors (well, some them anyway) become easy to see.

For more details, please see this page. Some of the papers are actually accessible even at the undergraduate level!